We recently released the final version of our contract projections for the 2019 NHL free agent class (they can be found here). Our initial projections went up in mid-April, and even though it’s only been a few weeks, we’ve had numerous questions about how the model was designed, how it works, what it means, etc. I thought we might be able to answer all the questions about it on twitter, but alas it was just a dream. A quick recap: this is our third year doing contract projections for the NHL offseason. While the model/projections this year may seem quite complicated, our first version was very simple: a few catch-all stats and a linear regression model to predict salary cap percentage (cap hit / salary cap). We use cap percentage to keep salaries on the same level as the salary cap changes. Over the last few years, we’ve developed a few new methods, and this year we took quite a bit of inspiration from the method Matt Cane used for his 2018 NHL offseason salary projections.
In the past, we chose to keep it simple and project only a given player’s cap percentage without contract length. But cap percentage alone is, obviously, only half of a player’s contract. Fans, analysts, teams, agents, players are concerned with both the cap hit of a contract and its length. Now it seems silly that one (or two) would even consider ignoring contract length given its significance. However, handling both a given contract’s length and value is quite a bit more complicated and involved than just predicting its value alone. Before we get into the reasons why this is, let’s first cover the data involved and how the model is constructed.
We’ve used data from the following sources:
- Salary Cap Information (CBA)
- NHL salary data (CapFriendly.com)
- Player information (NHL.com)
- Skater statistics (Evolving-Hockey.com)
First of all, we need to give a huge shoutout to CapFriendly. All salary information that was used to train our model was sourced from their website, which is fantastic. All other data is sourced from the NHL – technically we wrangled and “created” the stats for players (which are taken from our site above), but it all comes from the NHL. All of this data is joined together to prepare for model construction. For the contract, player info, and salary cap data this is fairly self-explanatory. For a given contract, we ensure that we also have each player’s age, draft round/position, height/weight, etc. along with the accompanying year’s salary cap figure.
However, the player stats that we use require a bit more work. When we initially started working on contract projections three years ago, we employed a weighting system similar to that of Tom Tango’s Marcel system without the regression. If a player signed July 1, 2018, we took a collection of stats for that player over their prior three years, computed a weighted average of those stats for the prior three years weighted by recency, and joined those weighted stats back in to the rest of the contract/player info data for the overall model dataset. As we’ve worked on our model over the last 3 years this method has stayed fairly consistent and works quite well. Let’s go back to the player above. Marcel utilizes 5/4/3 weights for years n-1, n-2, and n-3 (again, we’re ignoring the regression component here). For the player above, their ‘17-18 season stats receive a 5 weight (41.67%), ‘16-17 stats a 4 weight (33.33%), and ‘15-16 stats a 3 weight (25%). These weights are then applied to a number of metrics that (through testing) were found to be good predictors. These are then added to the existing contract and player info dataset. We’ll cover our weighting system below.
At this point, we have a big table of collected contracts, player data, and prior metrics that will ultimately be used to build a model that will predict future contracts. But how do we get from here to there? Predicting both contract length (“term” and “contract length” are used interchangeably) and cap percentage for a future contract requires a unique approach as contract length and contract value are separate problems. While money, in this sense, is a continuous number (say $650k all the way up to $12.5 million), term is categorical (there are only a set number of options or classes). We need two separate models for this task.
Term Model
As mentioned, the first step in the process is to create a model that will predict the length of a given future contract. The most recent CBA limited the max length of a contract to 8 years (Rule 50.8, subsection (b) (iv): “a Club may sign a Player to an SPC with a term of up to eight (8) years if that Player was on such Club’s Reserve List as of and since the most recent Trade Deadline.) However, prior to the ‘12/13 lockout, there were 15 players who signed contracts longer than 8 years. For the purpose of our model, we’ve treated these contracts as 8 year deals. With that adjustment, we’re left with 8 possible outcomes for a player’s contract length – these are the “classes” that make up our target or response variable.
Disclaimer: while I did just reference a section of the CBA which made me sound fancy, it’s important that I make it clear that we’re not NHL CBA or contract experts. Having worked with contracts for several years, I would say we’re quite familiar with how the CBA and contracts work but far from experts.
This type of problem is referred to as Multiclass Classification: “the problem of classifying instances into one of three or more classes”. While this may seem complicated, it’s similar to a problem that many sports fans are familiar with: what is the probability of a given team winning a particular game? This is “binary” classification – the target variable is either a 1 (true) or 0 (false). The model gives us a probability of an outcome being true (i.e. a 60% probability that the home team will win the future game). In multiclass classification, there are more possible outcomes than just 1 or 0. The model output generates probabilities for all classes (8 possible contract lengths in this case), and these all sum to 100%. Whichever length has the highest probability is the one that is selected. For instance, Artemi Panarin currently has a 41.8% chance of receiving an 8 year contract according to our current model, which is the term that we use for his final projection.
There are various algorithms that can deal with multiclass classification (Support Vector Machines, Neural Networks, K Nearest Neighbors, Naive Bayes, Decision Trees, Random Forests, Gradient Boosted Machines). After much testing, we (like Matt Cane) chose to use Random Forest to build our term model. While various other algorithms deal with multiclass classification well, this particular problem is unique. Not only do we have 8 total classes as possible outcomes, the distribution of the total number of contract lengths within each class is not distributed equally; this is an example of an imbalanced dataset. To demonstrate what this looks like, let’s take a look at the contract data from CapFriendly.
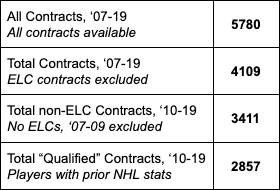
Remember, we’re only working with skater contracts (goalies… are goalies). We initially start out with 5780 contracts, but we exclude entry-level contracts (ELCs) and lose about 1600. We then remove the ‘07-08, ‘08-09, and ‘09-10 seasons. We’re using 3-year prior weights, which means any contract that was signed prior to the ‘10/11 season must be removed so we can develop our weights – all contracts must have equal information associated with them. Finally, any non-ELC contract that was signed after the ‘09/10 season for a player without prior year(s) stats is removed. The last remaining contracts that are removed are by and large seasoned AHL/non-NHL players who have no NHL time in the prior year(s) leading up to a given contract.
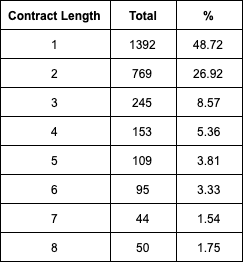
Now we can take a look at the imbalanced nature of the data. Here are the total number of contracts per length within the 2857 contracts that we were able to include in our model:
The same distribution of contract lengths applies season to season as well. Here’s a look at the average number of contracts signed within each of the 8 possible contract lengths using the data available for our model:
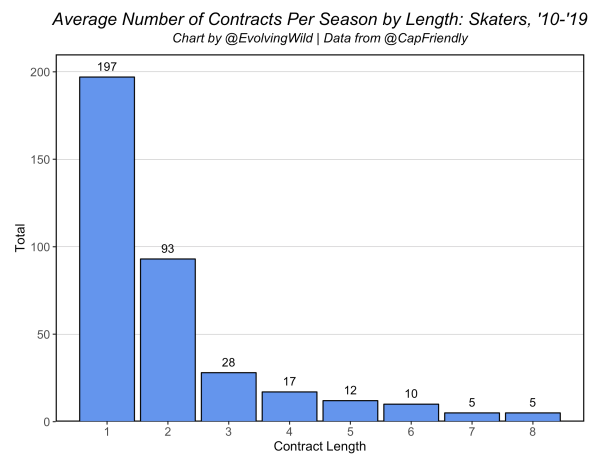
While the “big” contracts are the ones most pay attention to, the vast majority of all contracts that we are able to include are 1-2 year contracts (they make up roughly 75% of all contracts). And this, my friends, presents quite the problem (that imbalanced dataset thing I mentioned above). This might sound unique, but there are plenty of real-world scenarios where this exact issue presents itself. Fraud detection, medical diagnosis, text classification, and risk management (to name a few) are well-known problems that present similar imbalanced classes. While these seem somewhat commonplace, the skewed distribution of classes presents numerous problems.
When a dataset is imbalanced, the standard methods available to tune and train a given algorithm (resampling for instance ) do not accurately account for the class imbalance out of the box. For our problem (predicting contract length), historically nearly 75% of all contracts are either 1 or 2 years deals. So, if the model predicts only 1 or 2 year deals for all contracts, we’ll likely end up with a model that predicts some thing like 75% of all contract lengths correctly. Obviously this is simplistic (and maybe wrong), but a more extreme case might be fraud detection where ~99% of all observations are non-fraudulent – 99% accuracy is generally considered to be a great evaluation result, so if the model just selects “Not Fraud” for all predictions, it will have achieved an accuracy of 99%. However, the model will never predict classes that we care about (an instances of fraud, to keep with the example, or say any contract greater than 3 years). For more detail on imbalanced data/classes, please see this article.
As Jason Brownlee lays out here, there are various techniques available to help deal with the problems of class imbalance(s). I won’t cover all of them (acquiring more data, changing the evaluation metric, etc), but one of the best ways to deal with imbalanced data is to explore different algorithms. After exploration, we found Random Forest performed the best of any other model (we used R’s Ranger package just FYIl). However, it took quite a bit more work to deal with this imbalanced data. Ultimately we had to utilize something generally referred to as “class” or “case” weights. Synthetic sampling or subsampling is a common method that is utilized to help deal with class imbalances (under-sampling, over-sampling, SMOTE, ROSE here), and we tried all of these methods. However, none performed as well as weighting the classes based on distribution (classes are weighted inversely proportional to how frequently they appear link). Essentially, this penalizes misclassification of the infrequent classes more (contracts >2 years for instance) when tuning and building the (link), which ultimately proved to be a great method for this task.
With the model in place and the imbalanced data (more or less) accounted for, we can move on to the features/predictors in the term model. Here are the 3-year prior weighted-average metrics that were included in the term model. I’ll cover how these are weighted below.
Features (categorical):
- Position, age tier (see below), contract status (UFA/RFA), shoots (L/R), draft round (1-5, capped at 5), max_possible (see below),
Features (continuous):
- Years since draft, TOI, TOI %, G, A1, GS, iCF, ixG, giveaways, takeaways, 5v5 on-ice GF diff, 5v5 on-ice CF diff
Note: metrics are all situations unless noted
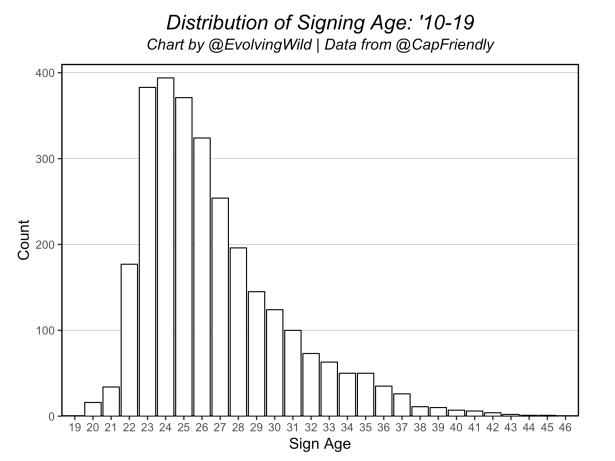
The above features in the model were selected via testing and tuning through various methods. As mentioned, most of the categorical features are static aspects connected to a player, and the continuous features (except for the years since draft feature) are the 3-year weighted stats from evolving-hockey.com. The “age tier” is a feature we created to deal with the number of possible ages for a given player. Even after we limit the contracts that can be included, there are still 26 total ages included in the data (20-45yo), and the distribution of these is not equal:
These are the age tiers included (yes I’m avoiding using “bins” to describe these for no reason whatsoever why would I do that):
Tier 1: <= 22
Tier 2: 23 & 24
Tier 3: 25 & 26
Tier 4: 27-29
Tier 5: 30-34
Tier 6: >= 35
And the resulting distribution of these new tiers looks like:
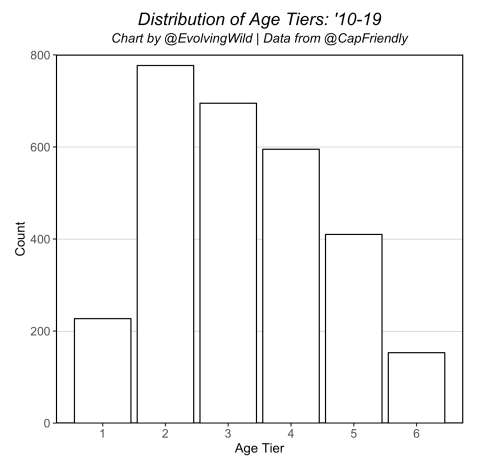
Now, separating age into tiers like this isn’t ideal, but the alternatives are worse. If we treat age as a continuous variable, the differences between relatively close but quite distinct ages (say 29 and 33) are too similar, and we see issues with players over say 35 years old re: exaggerated lengths (not that this isn’t still a small problem). If we use more tiers (say 8 or 9), the number of contracts within each becomes too small and the effect is extreme for young players. As mentioned, this extends further if we don’t combine ages at all. We found that the 6 tiers above worked as well as anything else we tried and kept important ages grouped together. But the downside to this is that we still inevitably have hard cutoffs between the tiers. For instance, the initial version had Kevin Hayes as a 26 year old (tier 3), but we had forgotten to update every player’s age to reflect the July 1st free agent date, and Hayes’ birthday is May 8th. As a result, he jumped up to tier 4, and both his term and money dropped because of this. But these are the small edge cases that you have to be ok with to improve overall performance.
As mentioned, we included a “max possible” feature for old players (mostly 35+ year olds). Initially, even with the age tiers working well, the model was still projecting unreasonable contract lengths for these old players (the model loved Justin Williams and loved to give him 7 years). In our data (qualified contracts), only three players 35 or older have signed a 4-year contract (Ed Jovanovski, Mark Streit, and Shane Doan), and only 10 players over 35 have signed 3-years contracts. Essentially, we created a binary feature that indicated whether it was possible for a player to sign a max-length contract. This handled these unreasonable projections well, but it’s not perfect (Williams is 37 and still projected at 3 years, Ron Hainsey is 38 and has a 2 year projection). But again, edge cases and whatnot. The term model was much more complicated than the cap percentage model, and each are linked to an extent. Let’s move on to that model, and we’ll cover a few more topics on term a bit later when we combine everything.
Cap Percentage Model
With the first part of our final model (term) complete, we move onto the cap percentage model. As I mentioned up front, cap percentage (cap hit / salary cap) is a continuous variable, which means we’ll use regression for this task. (We’re using the machine learning definitions here, so “regression” in this case refers to a target variable that is continuous as opposed to “classification” which is used for a discrete variable).
If we look at every contract in our dataset sorted by total cap percentage, we see a very distinct trend or distribution:
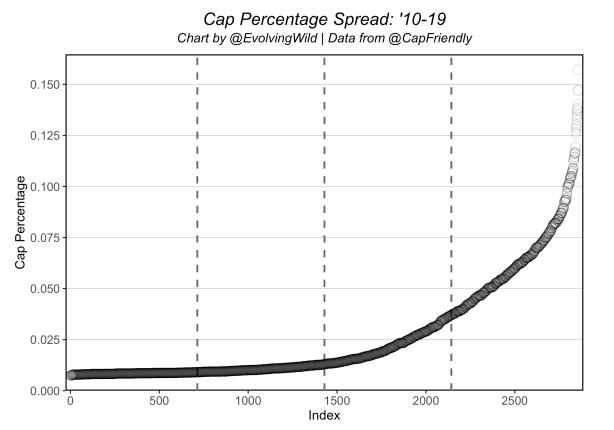
The gray dashed lines here are the 25% markers – 75% of all contracts included in our dataset are no greater than ~3.5% of the salary cap (~$3MM with an $83MM cap). So right away, algorithms that work well with linear/normal distributions like ordinary least squares regression (“linear regression”) will likely not be ideal. We need an algorithm that will better fit the distribution of our target variable. Again, we experimented with many algorithms, and found several that worked well with this type of distribution. MARS, tree-based models (random forest, GBMs), and SVM with radial basis kernel all worked quite well. But none worked as well or efficiently as an algorithm called “Cubist”. Based on Quinlan’s M5 model tree and ported from Ruelquest’s C5.0, Max Kuhn implemented this in R (specifically in the Caret package which he maintains). His vignette here gives a good overview of how and possibly why it works well for our current problem. Like MARS, Cubist is able to fit distributions like ours in a manner similar to MARS’ hinge functions (obviously they are not the same) via two parameters (Neighbors and Committees).
Like the term model, we use similar features to predict cap percentage:
Features (categorical):
- Term, position, age tier, contract status, shoots, draft round
Features (continuous):
- TOI, TOI %, G, A1, GS, iCF, iBLK, giveaways, takeaways, iPEND2, iPENT2, 5v5 on-ice GF diff
Notice the features are a bit different (for instance years since draft is no longer present, and it likely could be removed from the term model), but overall we’re using similar features to predict cap percentage. However, “term” is a feature now, which seems a bit odd. This is where the term model comes into play. We’ve chosen to include a “known” contract’s term as a feature in our cap percentage model. However, we can’t know how long a contract will be before we know what that contract’s cap hit is, right? They are signed simultaneously. However, when the cap percentage model is used to project a given player’s cap percentage, we will use that player’s projected term from the term model instead of what the term actually is. Let’s take a look at why we’ve chosen to approach cap percentage this way.
This table shows the relationship between contract length and cap percentage:
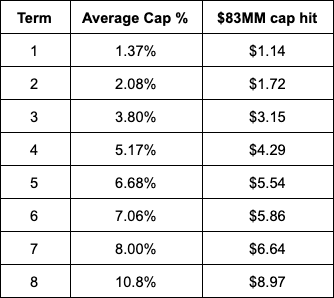
As term increases, cap percentage increase as well. For an even better view, let’s look at the densities of cap percentage for each term:
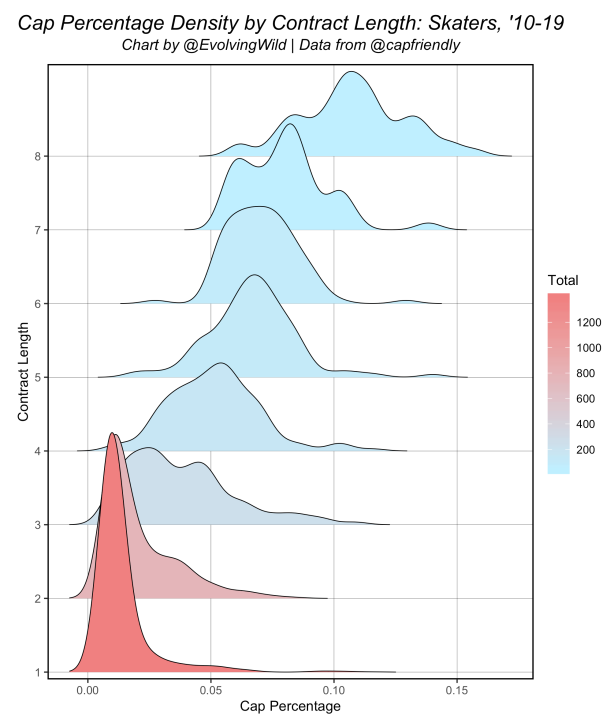
To put this in perspective, here are the lowest and highest cap percentages associated with each possible term/contract length:
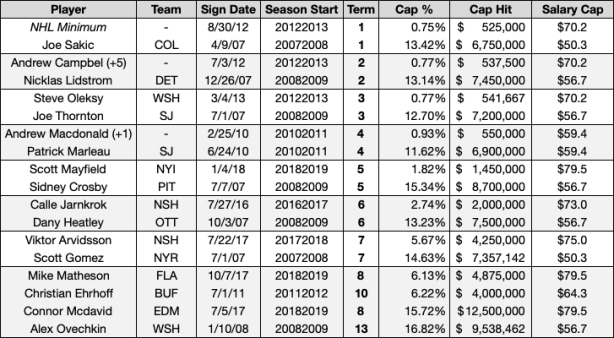
Including a contract’s term in the cap percentage model greatly improves the model’s ability to predict future cap percentage. As term increases cap percentage increases as well, and we see this relationship throughout the projections this year.
Metrics and Weights
Before I cover how the term and cap percentage models are combined to arrive at our final model, I need to cover both the important metrics and weighting method in each model. Both models utilize a very similar collection of prior metrics that are then weighted by recency to arrive at a 3-year weighted average for each. All metrics in each model receive the same weights as well, but they aren’t the same between each model. As we’ve already discussed in prior work, we generally aren’t fond of variable importance metrics to show which metrics are significant, but I’ll show it for simplicity. Here are the top 5 metrics for each model in terms of importance:
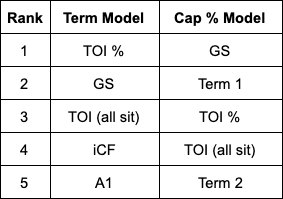
Now, there’s a lot more that’s going on within each model (each includes far more features than just the 5 here, and there are some issues with displaying and evaluating variable importance numbers when we’re working with this many categorical variables), but this essentially lines up with general consensus (just replace “Points” with “Game Score” and Paul Maurice’s quote still applies). Basically, players get paid based on their playing time and offense (game score / A1 / G). We’ve tried out various metrics over the years to account for defense or all-around player (like WAR), and the fact remains that GMs/teams do not pay players, overall, for their defense. A player who never gets injured, plays a lot of minutes, and “points” is one that teams love historically.
Moving on to the weights. We initially tried out the 5/4/3 weights for prior 3 years, and then switched to 6/3/1 after some preliminary testing. These weights were used for both models initially and worked well. But after some additional work, I finally succumbed to the temptation to run a very long grid search of various weights to see if we could improve how the prior years were being weighted. This was done by generating every combination of numbers between 1:20 over three columns. Like this: I then made sure that n-1 > n-2 > n-3 and selected every 46th row (out of 1140 rows) to arrive at 25 combinations of weights. With these 25 different sets of prior year weights in place, I trained 100 models (random forest and cubist) for each set of weights, evaluating various out of sample metrics for each set determine which performed the best. This was a lengthy process and could likely be optimized, but my computer was about ready to explode so we called that good (technically: this was a balance of time and necessity). Ultimately all we were looking to do was see if we could find a set of prior year weights that were “better” than the 6/3/1 weights we had been using. Luckily this actually did yield better results and was not for nothing.
I then made sure that n-1 > n-2 > n-3 and selected every 46th row (out of 1140 rows) to arrive at 25 combinations of weights. With these 25 different sets of prior year weights in place, I trained 100 models (random forest and cubist) for each set of weights, evaluating various out of sample metrics for each set determine which performed the best. This was a lengthy process and could likely be optimized, but my computer was about ready to explode so we called that good (technically: this was a balance of time and necessity). Ultimately all we were looking to do was see if we could find a set of prior year weights that were “better” than the 6/3/1 weights we had been using. Luckily this actually did yield better results and was not for nothing.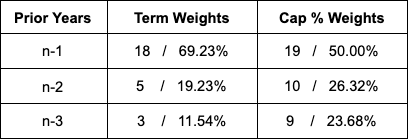 A note: the actual numbers here aren’t as important as the percentages (we could have used 6923 / 1923 / 1154 for instance and that would have produced the same result). What the above suggests is that for term, given a player’s info at the time a contract was signed and the metrics included, about 70% of the weight for those metrics should be assigned to the prior year (n-1), while only 30% (19/11) should be assigned to n-2 and n-3. For the cap percentage model however, only 50% of the weight should go to the prior year, and the n-2 and n-3 seasons should each get about the same amount of wait. Essentially, what we see here is an indication that GMs/teams place more weight on prior year performance (n-1) when determining how long a given contract should be. However, there is much more emphasis placed on a given player’s n-2 and n-3 years when determining cap percentage. Of course, the prior year is still the most important, but this was something that we found quite interesting.
A note: the actual numbers here aren’t as important as the percentages (we could have used 6923 / 1923 / 1154 for instance and that would have produced the same result). What the above suggests is that for term, given a player’s info at the time a contract was signed and the metrics included, about 70% of the weight for those metrics should be assigned to the prior year (n-1), while only 30% (19/11) should be assigned to n-2 and n-3. For the cap percentage model however, only 50% of the weight should go to the prior year, and the n-2 and n-3 seasons should each get about the same amount of wait. Essentially, what we see here is an indication that GMs/teams place more weight on prior year performance (n-1) when determining how long a given contract should be. However, there is much more emphasis placed on a given player’s n-2 and n-3 years when determining cap percentage. Of course, the prior year is still the most important, but this was something that we found quite interesting.
Final Model
Let us recap a bit. The final model consists of two sub-models (term and cap percentage). This final model gives us both cap percentage (in cap hit form – multiplied by $83MM) and the length of a given contract. To get this final projection, we actually have to predict the cap percentage for all possible terms (8) for all players. We do this by feeding the cap percentage model 1-8 contract lengths 8 times (for instance, the first run uses 1 year for the term feature in the cap percentage model for all players, the second run uses 2 years for all players, and so on). Once that is done, we select the cap percentage that corresponds with the given term the term model projected. The final google sheet that we’ve made available ((linked at the beginning of the article) also provides the probabilities for all 8 possible terms term along with the projected cap hit for the current projected $83MM salary cap, which are natural outputs of the term model (we don’t have to do anything special to get them).
With the final model in place, it’s important I cover some of the aspects we can’t account for or are unreasonable to account for. We have not included anything that considers other teammates on a given player’s team (for instance Mitch Marner’s contract in comparison to Auston Matthews’ or Klingberg and Lindell, etc). This type of situation is not very common and would most likely be a fairly insignificant feature in both underlying models. We have not included anything that would control for or determine whether a player will sign an 8 year deal (they sign with their current team) – this could be done with a separate model, but we didn’t go down that road. Additionally, we have not accounted for a given team’s market’s influence on contracts (think TOR vs. FLA) – again there might be something here, but it’s a long road that may or may not be fruitful. Finally (I think this is the last thing although I’m sure we’ll get yelled for something we’ve missed), we do not have anything that deals with arbitration.
I think it’s fair to treat our final projections as environment neutral. We’ve attempted to isolate individual players and build a model that will project what we might expect a player’s next contract to be based on historic results. It’s important to remember that NHL general managers value players differently than fans or analysts or statisticians. These projections are based on what GMs have paid players in the past – everything included in the model is set up and calibrated to best predict this relationship. Please feel free to reach out if you have any questions or comments! We can be found on twitter (@EvolvingWild), through email (evolvingwild at gmail dot com), or in the comments below.

This was fantastic. I loved that you shared your approach to dealing with the data’s integrity when building a purposeful dataset for your models. And the way you came to 18-5-3/19-10-9, despite repeatedly warning exploration may be fruitless, felt like a triumph to me as the reader.
I really loved this article and the spreadsheet. Super helpful! There might be something I’m not seeing or thinking about, but can there be a cap difference based on the number of years signed column? The current Cap difference column makes some contracts look like a very big steal based on the fact that the projected cap hit was for a much longer term and vise versa. A good example of this would be Brandon Carlo who was projected for 6 years at 4.235 million, but ended up signing for 2 years at 2.85 million. But looking at your projected cap hit at a given length category, it was projected that at 2 years Carlo should get around 2.6 million, a much less cap difference then indicated. For me, that would’ve been very helpful, but overall, this is a very cool and helpful tool for all hockey fans!
Is there a reason you didn’t round your predicted values to the nearest 5000? or 10000?